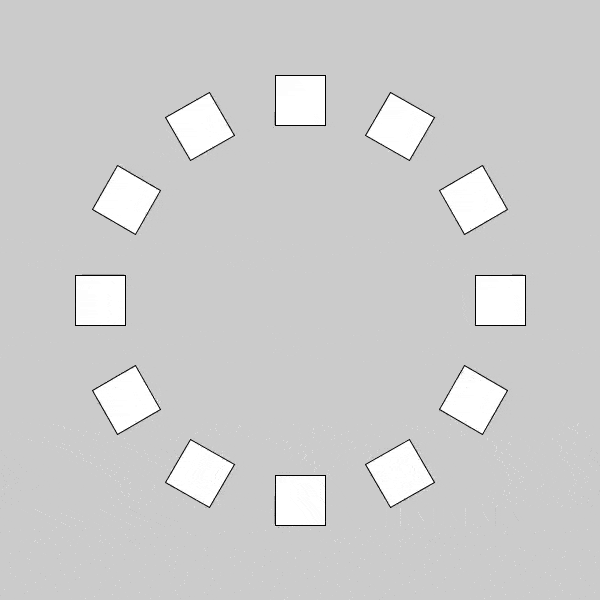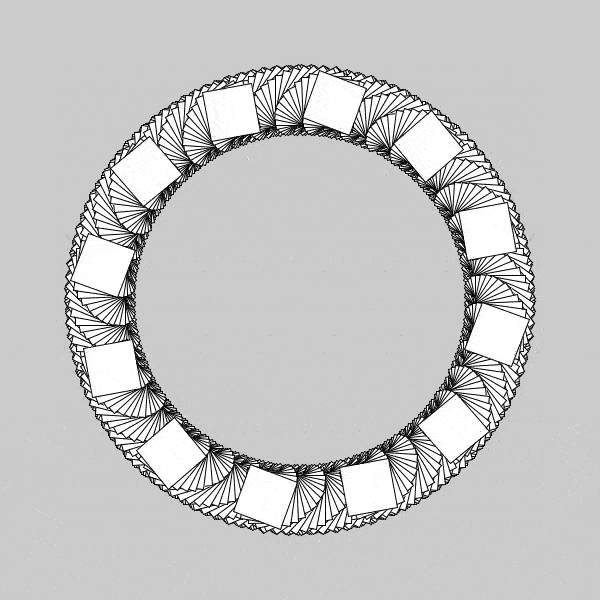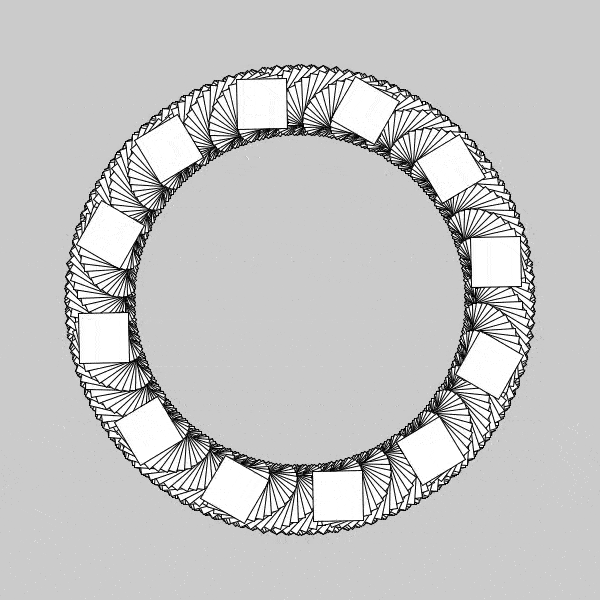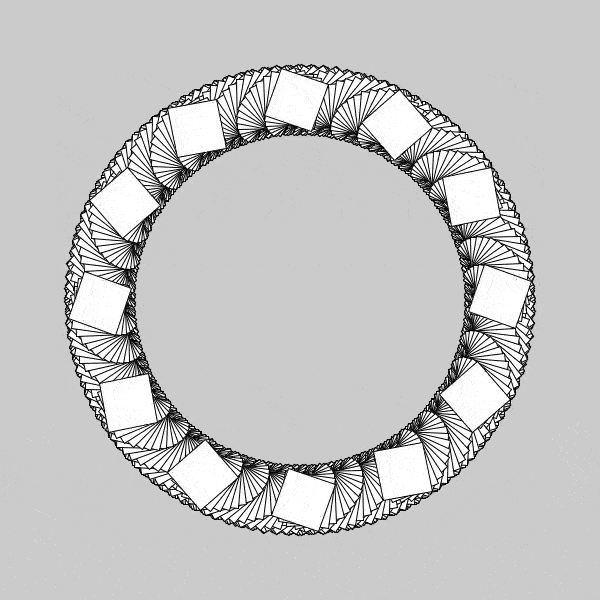
How complex are patterns formed by spinning squares? Not really a question often brought up in conversation, but let’s have some fun with it. I got to thinking, if I took some squares, arranged them in a circle on a table, and spun the table, I should see them perfectly map out a circle. Easy enough to test with enough post-it notes, and sure enough, it’s a circle. Not too surprising. But then I thought, what about if I spun each square individually as I spun the table? I would also want to be able to trace out the path left by each square in order to see a pattern, doing that experiment without regards to tracing is an easy enough thought experiment, but I want to know what patterns it may make. If I had too much time on my hands to build a fancy machine to do this for me, or if I had too many hands I could spin all the squares and trace them at the same time, but neither is true so I resorted to our old friend the computer. In Processing I made my circle of squares, and spun them at the same rate I spun the “table” (my coordinates, in this case), and wound up with the following.

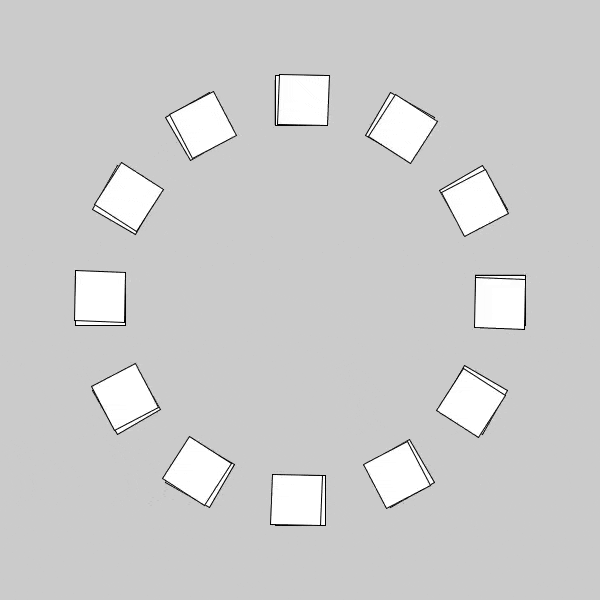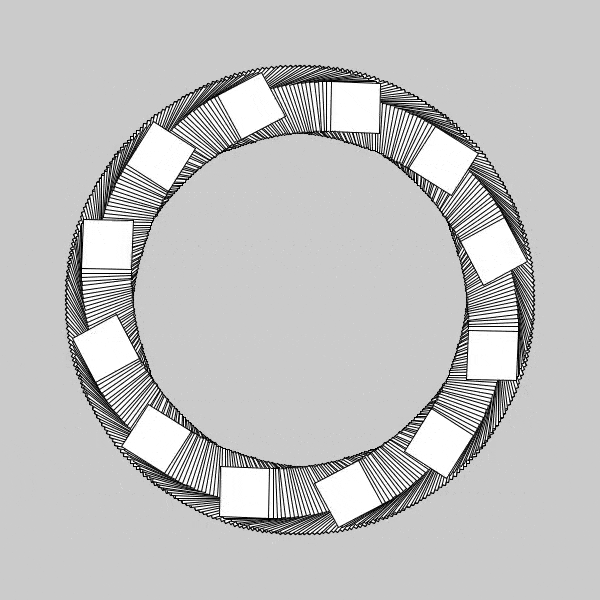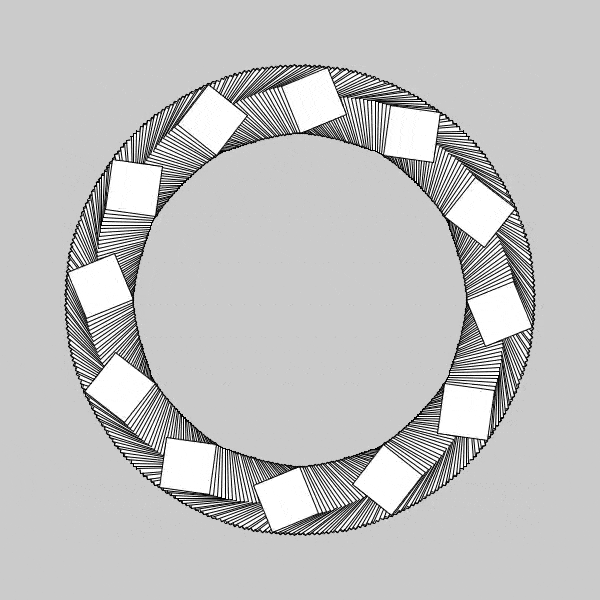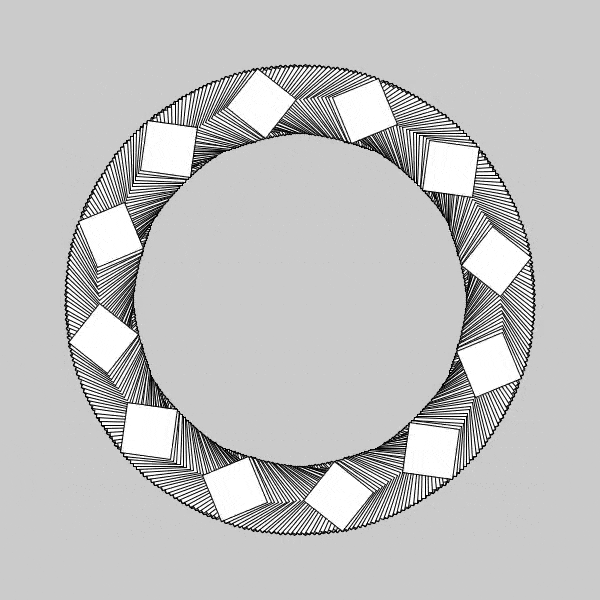
Now that’s cool, even if it’s expected. We can see the corners of the squares trace out circles with progressively increasing radii as the individual square tracks the corner along from inside to outside. In spinning the individual squares while spinning the coordinate space on which they are situated, it is incredibly clear that we create a ring with width being sqrt(2)*sidelength of the square. I thought to myself, naturally, we now have a maximum ring size, but if I change the rate of rotation of the squares with respect to the total rotation, what types of inner patterns will this create(similar to the tracing of the corners)? Well, I began by spinning my table(coordinates) at a great speed compared to that of the individual squares rate of rotation, and sure enough ended up with a different pattern.

Now that’s neat. I managed to get the speed just correct so that way there appears to be no spinning of the table, but have tripled the amount of squares present. Of course, the actual number of squares is the same as the above, but it is now spinning fast enough that it can’t be distinguished. Also, since they don’t appear to move, each individual square maps out its own circle(3 times), creating a “braided” appearance. After that question was answered, I naturally wanted to see the opposite,

Now, with the individual squares spinning much faster than the table, we are able to more clearly see the arcs that each square maps out during its rotations. The speed of rotation is not perfect, as the previous one, but nearly. You can see the inner radius of our “donut” slowly get populated more and more as time progresses, which I believe if I found the perfect angles of rotation, I could get it to maintain its first initial seashell spiral pattern throughout its entirety. I was still curious regarding these squares, and wanted to see where I could go next. I found a great question in asking whether my patterns would change if I simply changed the pivot location of the individual squares, my guess was yes, but really I wanted to know what types of patterns this would make. I did this, same procedure as above, and found some really interesting behavior, and will likely be posting about that in the next day or so, so stay posted!